Problem on circuits

Problem on circuit theory

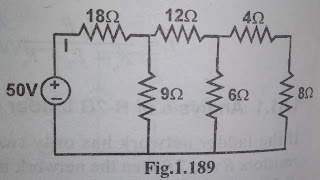
Find all branch currents, branch voltages and power dissipated in each resistor for the circuit shown in figure 1.189.

Solution :-

From figure 1.190. we can find

Rx=(8+4)||6
     =12||6
     =(12×6)/(12+6)
     =4 ohms

Ry=(Rx+12)||9
     =16||9
     =(16×9)/(16+9)
     =5.76 ohms

Req=18+Ry=18+5.76=23.76 ohms

Current, I =50/Req=50/23.76=2.104A

The branch current,
I1=I×(12+Rx)/9+12+Rx
    =(2.102)(16)/(21+4)=1.3468A

The branch current,
I2=I×(9)/(9+12+Rx)
    =(2.104)(9)/(21+4)= 0.7575 A

The branch current,
I3=(I2)(8+4)/(8+4+6)
    =(0.7575)(12)/18= 0.505 A

The branch current,
I4=(I2)(6)/(8+4+6)=0.2525 A

The voltage across 18 ohms resistance,
V18=(I)(18)=(2.104)(18)=37.878 V

The power dissipated in 18 ohms resistance
P18=I^2(R)=(2.104)^2(18)=79.711 W

The voltage across 9 ohms resistance,
V9 =(I1)(9)=(1.3468)(9)=12.1212 V

The power dissipated,
P9=(I1)^2(9)=(1.3468)^2(9)=16.3248 W

The voltage across 12 ohms resistance,
V12=(I2)(12)=(0.7575)(12)=9.09 V

The power dissipated,
P12=(I2)^2(12)=(0.7575)^2(12)=6.8856 W

The voltage across 6ohms resistance
V6=(I3)(6)=(0.505)(6)=3.03 V

The power dissipated
P6=(I3)^2(6)=(0.505)^2(6)=1.53 W

The voltage across 4ohms resistance
V4=(I4)(4)=(0.2525)(4)=1.01 V

The power dissipated,
P4=(I4)^2(4)=(0.2525)^2(4)=0.255 W

The voltage across 8ohms resistance
V8=(I4)(8)=(0.2525)(8)=2.02 V

The power dissipated
P8 =(I4)^2(8)=(0.2525)^2(8)=0.510 W

For clear solution :-

👍👍 ALL THE BEST 👍👍

Please Like and share